かんとこうブログ

昨日はさくらの開花予想に関する「魔法式」があり、それが「アレニウス式」に似ているというところまで書きました。今日はこの続きです。世の中は新コロナ一色ですが、ひと時忘れて桜の花を思い浮かべながら読んでください。

魔法式は　Σexp(Ea*(T-Ts))/(R*T*Ts)=23.8　でした。 ここでEaは活性化エネルギー、Rはガス定数、Tはその日の日平均温度、Tsは基準温度です。この魔法式を少し書き換えてみるとアレニウス式に似ていることが良くわかります。左辺は以下のように書き換えることができます。Σexp(Ea*(T-Ts))/(R*T*Ts)＝Σexp((E/RT)*(T/Ts-1))

　一方アレニウス式は　ｋ＝A exp(-E/RT)  ここでｋは反応速度定数、Aは頻度因子(定数)、Eは活性化エネルギー、Rはガス定数、Tは温度です。スウエーデンの化学者、アレニウスによって提唱された化学反応速度に関する式であることは、化学を学んだ人であれば誰でも知っていることでしょう。書き換えた式「魔法式」の(E/RT)は正負の違いはあれアレニウスの式の(-E/RT)と同じであり、（Ｔ/Ｔｓ-1）はその温度補正項とみなすことができます。

ちなみに後半の温度補正項は、基準温度を一般的な15℃とすれば、2月、3月では日平均温度は15℃より低いので、かならずマイナスとなります。温度補正項は温度の一次関数に、魔法式左辺exp(Ea*(T-Ts))/(R*T*Ts)は温度の指数関数になります。興味のある方は、

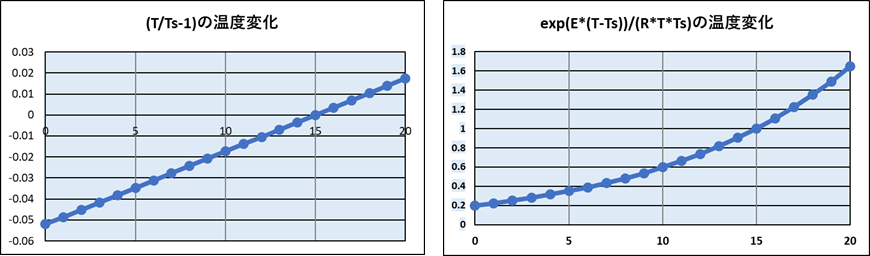
青野教授らは、全国の多数の地点で実際の気象条件と桜の開花日を「魔法式」による予想日とともに検証し、この両者を良い精度で一致させることができたとしています。

　長々と書いてきましたが、このブログを書こうと思った理由は、「桜の開花」のような自然現象が、実は化学反応の速度定数を求める式と同じ考え方で予測できるということに感動を覚えたからです。この「温度変換日数法」は桜だけでなく様々な植物の開花予想に使用されています。アレニウス式は、化学反応速度のみならず、植物の成長予測にも有効なのです。

　翻って塗料に思いをはせれば、貯蔵安定性試験や促進試験など、温度条件を変動させて塗料の試験を行う機会はたくさんありますが、もちろん、そうした試験が実施されている背景にはこのアレニウス式の存在があります。日々の業務の中でとかくこのことを忘れがちになりますが、桜の開花すら律するこのアレニウス式を、温度条件を変動した試験を行うたびに思いだしてその意義を確認してもらえたら良いなと思います。

河津川両岸を埋め尽くす河津桜の威容

このブログを書くにあたり以下のサイトの情報を参考にさせてもらいました。

https://weathernews.jp/s/topics/201802/150105/

https://withnews.jp/article/f0180319001qq000000000000000W08e10701qq000016960A

https://www.jstage.jst.go.jp/article/agrmet1943/52/2/52_2_125/_pdf/-char/en

http://www1.ous.ac.jp/garden/kenkyuhoukoku/13/Naturalistae13-1-7.pdf