かんとこうブログ

第８波は果たして新年にむけて急拡大するのか、このまま緩やかに拡大し続けるのかとても気になるところです。私としては、感染拡大速度の指標としては実効再生産数が最も適していると考えており、これまで実効再生産数を使って、第8波の感染拡大スピードが第7波に比べてとても緩やかであると紹介してきました。

一方マスメディアでは、実効再生産数の数値が紹介されることはほとんどなく、7日間平均またその日の新規感染者数について1週間前の同じ曜日の新規感染者数との比率を使って感染拡大の状況を紹介するケースが多いようです。今日はこの両者がどのような関係にあるのかについてご紹介した上で、さらに実効再生産数が変化すると今後の新規感染者数がどのように変化かを予測してみました。

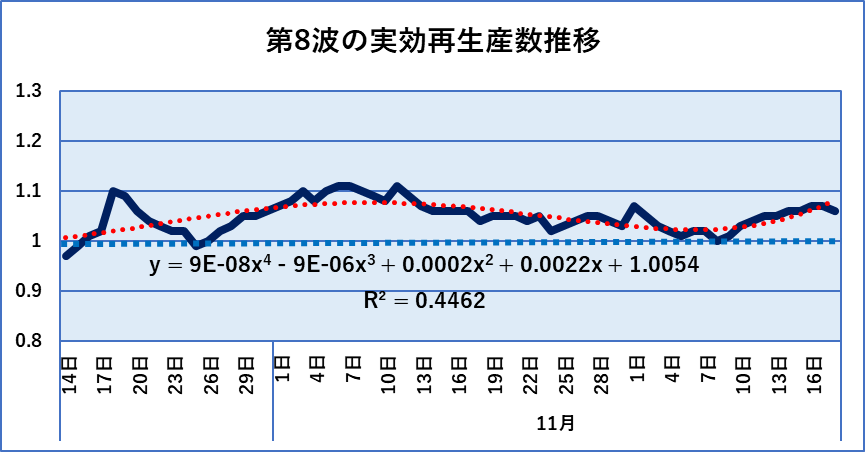
私はこれまで実効再生産数については、ずっと東洋経済新聞社のサイトの数字を引用させてもらっています。また新規感染者数については、同サイトの7日間平均の新規感染者数の数字を引用させてもらっていました。これらの数値を使って、7日間平均の新規感染者数と1週間前の7日間平均の新規感染者数との比率（以下1週間前比と略す）と実効再生産数の両者の推移を同じグラフで表すと以下のようになります。（期間は10月14日から12月18日まで）

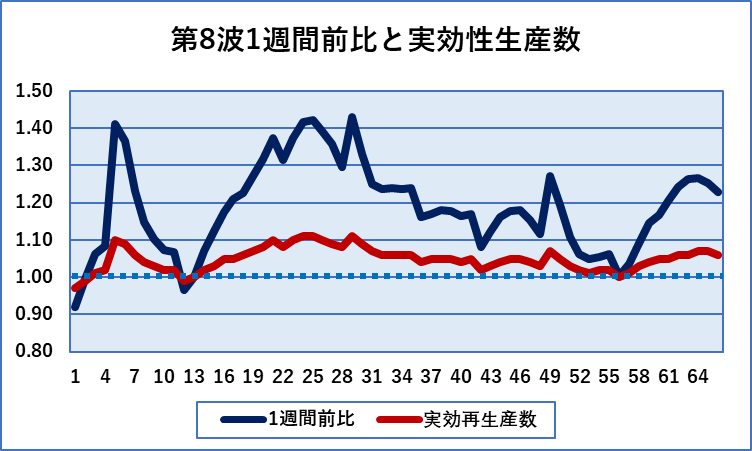
この2本の線は振幅こそ違いますが、連動して上下していることがわかります。そこで、振幅が同じくなるように描いてみることにしました。実効再生産数の振幅を4倍に拡大すると下図左のようにぴったりと両者が重なることがわかりました。

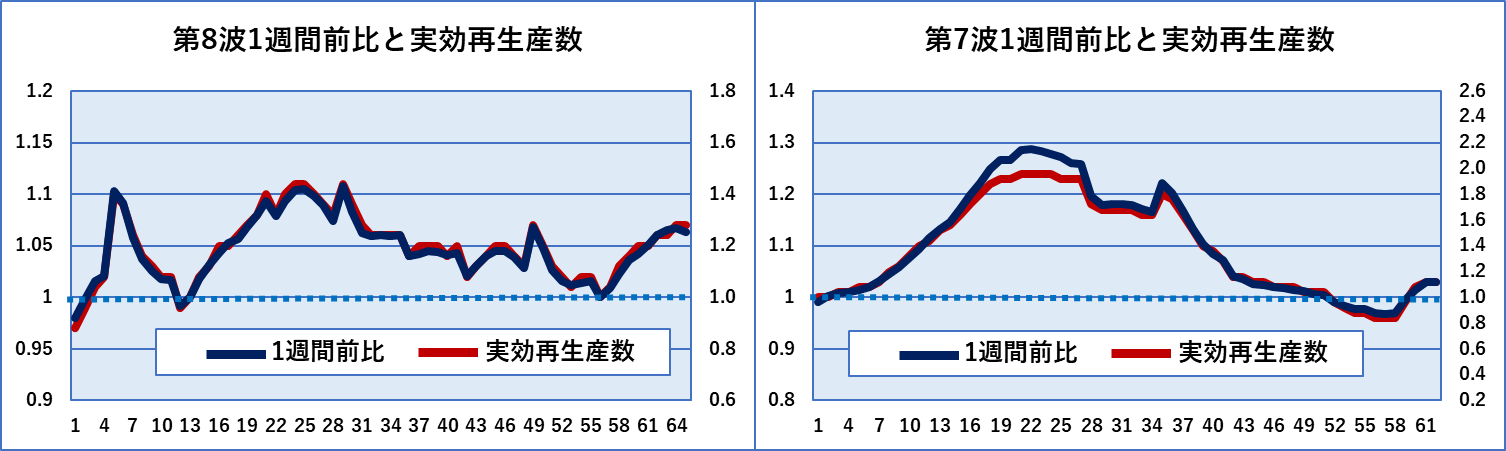
また第7波についても実効再生産数を振れ幅を4倍にすれば、実効再生産数が1.2よりも高いところを除きほぼ一致することがわかります。このように書くと大発見のようですが、改めて実効再生産数の計算式を見ると一致するのが当然であることがわかりました。東洋経済新聞社のコロナ特設サイトに記載してある実効再生産数の計算式は以下のようになります。

実効再生産数＝（直近7日間の新規陽性者数／その前7日間の新規陽性者数）^（平均世代時間／報告間隔）ここで平均世代時間は2日、 報告間隔は7日と仮定しているので実際の計算式は

実効再生産数＝（直近7日間の新規陽性者数／その前7日間の新規陽性者数）^(2/7)となります。

計算式右辺の第1項は、実は1週間前比（7日間平均の新規感染者数と1週間前の7日間平均の新規感染者数との比率）そのものなのです。つまり、実効再生産数＝(1週間前比)＾(2/7)　ということになります。さらにαが十分に小さいときは、(1＋α)＾ｎ≒1+ｎα　であるので、最終的に　実行再生産数≒1+(2/7*(１週間前比-1))となります。

この式を使えば、実効再生産数の数値から新規感染者数を簡単に予測できます。

上のグラフでは、実効再生産数の振れ幅を4倍にしました。3.5倍にすればさらに一致するものと思われますが、第1軸、第2軸をそろえて書くのが難しかったので4倍のままにしてあります。計算するだけなら3.5倍にして計算することは容易ですので、仮に実効再生産数が1.05（ほぼ現在のレベル）から0.05刻みで上昇した場合の３週間後の新規感染者数を予測してみました。結果を下図に示します。

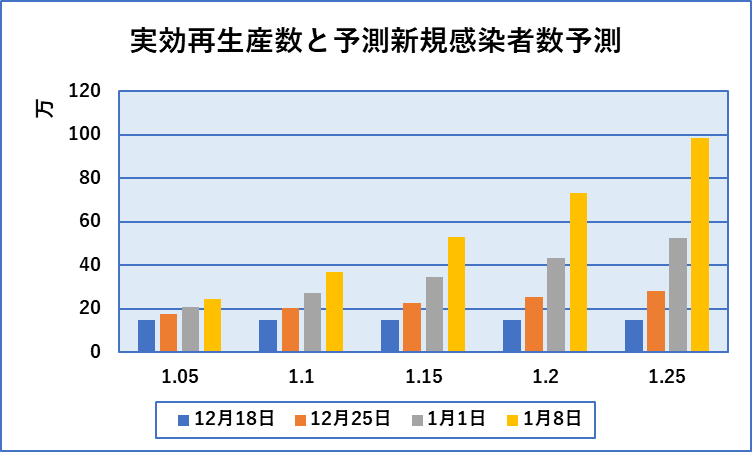
横軸は実効再生産数で、12月18日現在は1.06です。仮にこのまま実効再生産数が1.05であれば新規感染者数が3週間後に現在の1.6倍になるだけですが、0.05上昇して1.10になると3週間後には現在の2.5倍、1.15では現在の3.5倍、1.20だと現在の4.9倍、1.25では現在の6.6倍と急速に感染が拡大していきます。実効再生産数のわずかな上昇が空隙な感染者増加につながるということです。

第8波はこれまで新規感染者数が急増しなかったため実効再生産数の推移もほぼ横ばいであり、1.0から1.1の間を推移してきました。今後ともこのような動きであってほしいと思わずにはいられません。また、昨年のような年末からの急拡大だけはなんとしても避けたいと強く願うところです。