かんとこうブログ
2021.06.14
すでに増加の兆し・・東京の新規感染者数と実効再生産数
一昨日の土曜日に、東京の新規感染者数が久しぶりに前の週を上回ったと報じられました。専門家の間では再拡大の懸念が表明されています。今日は最近の新規感染者の推移から、純粋に数学的方法で近似式をもとめ6月末時点での感染者数を予想するとともに、実効再生産数についても同様に計算してみます。
まずは、1月から6月までの東京都の新規感染者数の推移をご覧ください。
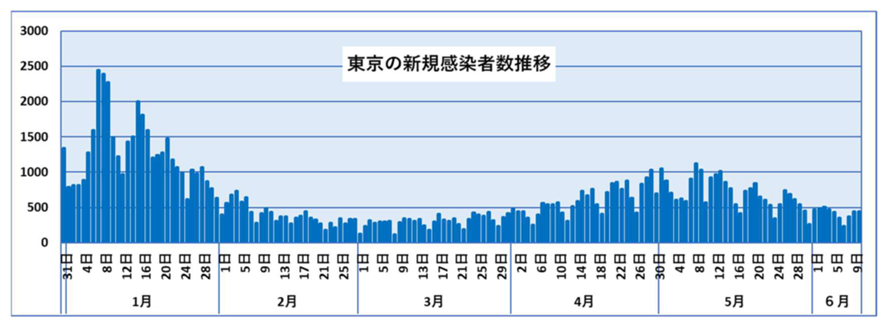
最近の1週間があまり減っていないように見えますが、全体としては減少傾向の途中にあるように見えます。次にこれを最近30日について詳しく表示し、近似線を求めた結果をご紹介します。
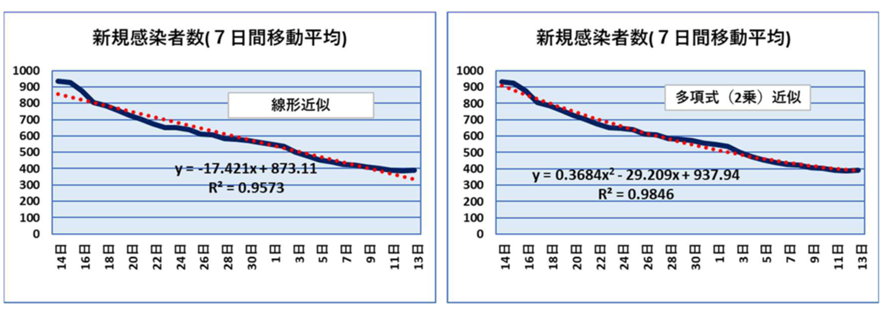 左は直線近似、右は多項式(2乗)近似です。いずれもよく近似されており、R2乗値は高い数字になっていますが、多項式近似(2乗近似)の方が高い数値になっています。問題は、多項式近似の場合には、2乗項の係数が正なのでこのあとどこかで極小値をとりそれから上昇するということです。近似式から計算される極小値の日にちは6月22日と計算されます。そして新規感染者数は6月末で379人、7月末では901人と計算されます。
左は直線近似、右は多項式(2乗)近似です。いずれもよく近似されており、R2乗値は高い数字になっていますが、多項式近似(2乗近似)の方が高い数値になっています。問題は、多項式近似の場合には、2乗項の係数が正なのでこのあとどこかで極小値をとりそれから上昇するということです。近似式から計算される極小値の日にちは6月22日と計算されます。そして新規感染者数は6月末で379人、7月末では901人と計算されます。
左の直線近似では、6月末の新規感染者数はマイナスとなり、直線近似以外でも、累乗近似はじめ多項式近似以外はマイナスの予想値になります。ここで思いだしたのが3月時点での新規感染者予想です。同様なことを行い、最もR2乗値の高かった多項式近似だけが感染拡大を予想し、事実その通りになりました。今回のそうならないとよいのですが・・
実効再生産数についても同じことをしてみました。最近1か月(といっても計算可能な5月1日から5月31日まで)の実効再生産数の推移と代表的な近似式を下に示します。
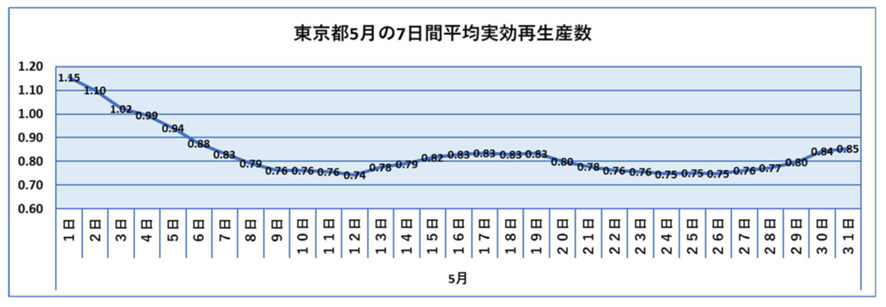
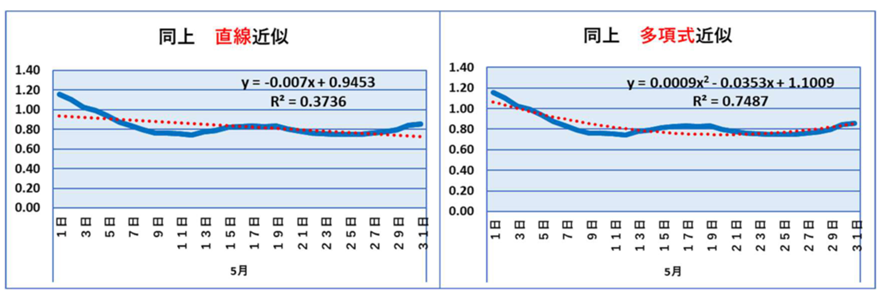
実効再生産数は、実は5月に入り5月12日に底を打ったあと、一度増加に転じ、再び減少し5月24-25日に底をうち、その後増加しています。昨日の時点では5月31日までしか計算できませんのでこれをもとに計算してみます。
近似の結果を示します。左が直線近似、右が多項式近似です。R2乗値をみてもらうと歴然です。多項式近似の方が高い、すなわちよく近似されているということになります。多項式近似の近似式(二次式)では、極小値は5月19日になりますので、それ以降は増加の一途であり、6月末ではなんと2.37になります。2.37という数値はこれまで出現した実際の数値としては最高の部類になります。
いかがでしょうか?これは単なる数学的な近似計算にすぎません。がしかし、明日ご紹介するように、4月25日の緊急事態宣言発出後に、激減した東京都の人流はすぐに4月25日前に戻りました。となれば感染拡大は時間の問題であるというのが結論です。オリンピックはどうあっても開催されるようですが、6月22日に迎える緊急事態宣言の期間終了に際し、根拠のない楽観論と精神論だけでなし崩し的な解除をしないよう強く主張したいと思います。